토픽 모델링(Topic Modeling)이란 기계 학습 및 자연어 처리 분야에서 토픽이라는 문서 집합의 추상적인 주제를 발견하기 위한 통계적 모델 중 하나로, 텍스트 본문의 숨겨진 의미 구조를 발견하기 위해 사용되는 텍스트 마이닝 기법이다.
1) 잠재 의미 분석(Latent Semantic Analysis, LSA)
BoW에 기반한 DTM이나 TF-IDF는 기본적으로 단어의 빈도 수를 이용한 수치화 방법이기 때문에 단어의 의미를 고려하지 못한다는 단점이 있다. 이를 위한 대안으로 DTM의 잠재된(Latent) 의미를 이끌어내는 방법으로 잠재 의미 분석(Latent Semantic Analysis, LSA)이라는 방법이 있다. 잠재 의미 분석(Latent Semantic Indexing, LSI)이라고 부르기도 한니다.
이 방법을 이해하기 위해서는 선형대수학의 특이값 분해(Singular Value Decomposition, SVD)를 이해할 필요가 있다.
1. 특이값 분해(Singular Value Decomposition, SVD)
시작하기 앞서, 여기서의 특이값 분해(Singular Value Decomposition, SVD)는 실수 벡터 공간에 한정하여 내용을 설명함을 명시한다. SVD란 A가 m × n 행렬일 때, 다음과 같이 3개의 행렬의 곱으로 분해(decomposition)하는 것을 말한다.

여기서 각 3개의 행렬은 다음과 같은 조건을 만족한다.

여기서 직교행렬(orthogonal matrix)이란 자신과 자신의 전치 행렬(transposed matrix)의 곱 또는 이를 반대로 곱한 결과가 단위행렬(identity matrix)이 되는 행렬을 말한다. 또한 대각행렬(diagonal matrix)이란 주대각선을 제외한 곳의 원소가 모두 0인 행렬을 의미한다.
이때 SVD로 나온 대각 행렬의 대각 원소의 값을 행렬 A의 특이값(singular value)라고 한다.
2. 절단된 SVD(Truncated SVD)
위에서 설명한 SVD를 풀 SVD(full SVD)라고 한다. 하지만 LSA의 경우 풀 SVD에서 나온 3개의 행렬에서 일부 벡터들을 삭제시킨 절단된 SVD(truncated SVD)를 사용한다.

절단된 SVD는 대각 행렬 Σ의 대각 원소의 값 중에서 상위값 t개만 남는다.
절단된 SVD를 수행하면 값의 손실이 일어나므로 기존의 행렬 A를 복구할 수 없다.
또한, U행렬과 V행렬의 t열까지만 남긴다. 여기서 t는 우리가 찾고자하는 토픽의 수를 반영한 하이퍼파라미터값이다. 하이퍼파라미터란 사용자가 직접 값을 선택하며 성능에 영향을 주는 매개변수를 말한다.
t를 크게 잡으면 기존의 행렬 A로부터 다양한 의미를 가져갈 수 있지만, t를 작게 잡아야만 노이즈를 제거할 수 있다.
이렇게 일부 벡터들을 삭제하는 것을 데이터의 차원을 줄인다고도 말하는데, 데이터의 차원을 줄이게되면 당연히 풀 SVD를 하였을 때보다 직관적으로 계산 비용이 낮아지는 효과를 얻을 수 있다.
계산 비용이 낮아지는 것 외에도 상대적으로 중요하지 않은 정보를 삭제하는 효과를 갖고 있는데, 이는 영상 처리 분야에서는 노이즈를 제거한다는 의미를 갖고 자연어 처리 분야에서는 설명력이 낮은 정보를 삭제하고 설명력이 높은 정보를 남긴다는 의미를 갖고 있다. 즉, 다시 말하면 기존의 행렬에서는 드러나지 않았던 심층적인 의미를 확인할 수 있게 해준다.
3. 잠재 의미 분석(Latent Semantic Analysis, LSA)
축소된 SVD는 문서의 개수 × 토픽의 수 t의 크기를 가진다. 단어의 개수는 유지되지 않는다.
U의 각 행은 잠재 의미를 표현하기 위한 수치화 된 각각의 문서 벡터라고 볼 수 있다. 축소된 VT는 토픽의 수 t × 단어의 개수의 크기이다. VT의 각 열은 잠재 의미를 표현하기 위해 수치화된 각각의 단어 벡터라고 볼 수 있다.
이 문서 벡터들과 단어 벡터들을 통해 다른 문서의 유사도, 다른 단어의 유사도, 단어(쿼리)로부터 문서의 유사도를 구하는 것들이 가능해진다.
4. LSA의 장단점(Pros and Cons of LSA)
정리해보면 LSA는 쉽고 빠르게 구현이 가능할 뿐만 아니라 단어의 잠재적인 의미를 이끌어낼 수 있어 문서의 유사도 계산 등에서 좋은 성능을 보여준다는 장점을 갖고 있다. 하지만 SVD의 특성상 이미 계산된 LSA에 새로운 데이터를 추가하여 계산하려고하면 보통 처음부터 다시 계산해야 한다. 즉, 새로운 정보에 대해 업데이트가 어렵다. 이는 최근 LSA 대신 Word2Vec 등 단어의 의미를 벡터화할 수 있는 또 다른 방법론인 인공 신경망 기반의 방법론이 각광받는 이유이기도 하다.
2) 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)
토픽 모델링은 문서의 집합에서 토픽을 찾아내는 프로세스를 말한다. 이는 검색 엔진, 고객 민원 시스템 등과 같이 문서의 주제를 알아내는 일이 중요한 곳에서 사용돤다. 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)은 토픽 모델링의 대표적인 알고리즘이다.
LDA는 문서들은 토픽들의 혼합으로 구성되어져 있으며, 토픽들은 확률 분포에 기반하여 단어들을 생성한다고 가정한다. 데이터가 주어지면, LDA는 문서가 생성되던 과정을 역추적한다.
1. LDA의 가정
LDA는 문서의 집합으로부터 어떤 토픽이 존재하는지를 알아내기 위한 알고리즘이다. LDA는 빈도수 기반의 표현 방법인 BoW의 행렬 DTM 또는 TF-IDF 행렬을 입력으로 하는데, 이로부터 알 수 있는 사실은 LDA는 단어의 순서는 신경쓰지 않겠다는 것이다.
LDA는 문서들로부터 토픽을 뽑아내기 위해서 각각의 문서는 다음과 같은 과정을 거쳐서 작성되었다고 가정한다.
1) 문서에 사용할 단어의 개수 N을 정한다.
2) 문서에 사용할 토픽의 혼합을 확률 분포에 기반하여 결정한다.
- Ex) 토픽이 2개라고 하였을 때 강아지 토픽을 60%, 과일 토픽을 40%와 같이 선택할 수 있다.
3) 문서에 사용할 각 단어를 (아래와 같이) 정한다.
3-1) 토픽 분포에서 토픽 T를 확률적으로 고른다.
- Ex) 60% 확률로 강아지 토픽을 선택하고, 40% 확률로 과일 토픽을 선택할 수 있다.
3-2) 선택한 토픽 T에서 단어의 출현 확률 분포에 기반해 문서에 사용할 단어를 고릅니다.
- Ex) 강아지 토픽을 선택하였다면, 33% 확률로 강아지란 단어를 선택할 수 있다. 이제 3)을 반복하면서 문서를
완성한다.
이러한 과정을 통해 문서가 작성되었다는 가정 하에 LDA는 토픽을 뽑아내기 위하여 위 과정을 역으로 추적하는 역공학(reverse engneering)을 수행한다.
2. LDA의 수행하기
1) 사용자는 알고리즘에게 토픽의 개수 k를 알려줍니다.
LDA는 토픽의 개수 k를 입력받으면, k개의 토픽이 M개의 전체 문서에 걸쳐 분포되어 있다고 가정한다.
2) 모든 단어를 k개 중 하나의 토픽에 할당한다.
LDA는 모든 문서의 모든 단어에 대해서 k개 중 하나의 토픽을 랜덤으로 할당한다.
이 작업이 끝나면 각 문서는 토픽을 가지며, 토픽은 단어 분포를 가지는 상태이다.
물론 랜덤으로 할당하였기 때문에 사실 이 결과는 전부 틀린 상태이다.
3) 이제 모든 문서의 모든 단어에 대해서 아래의 사항을 반복 진행한다. (iterative)
3-1) 어떤 문서의 각 단어 w는 자신은 잘못된 토픽에 할당되어져 있지만,
다른 단어들은 전부 올바른 토픽에 할당되어져 있는 상태라고 가정한다.
이에 따라 단어 w는 아래의 두 가지 기준에 따라서 토픽이 재할당된다.
- p(topic t | document d) : 문서 d의 단어들 중 토픽 t에 해당하는 단어들의 비율
- p(word w | topic t) : 각 토픽들 t에서 해당 단어 w의 분포
이를 반복하면, 모든 할당이 완료된 수렴 상태가 된다.
두 가지 기준이 어떤 의미인지 예를 들어보자.
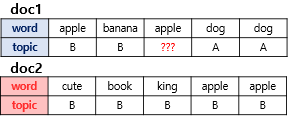
위의 그림은 두 개의 문서 doc1과 doc2를 보여준다. 여기서는 doc1의 세번째 단어 apple의 토픽을 결정하고자 한다.

우선 첫번째로 사용하는 기준은 문서 doc1의 단어들이 어떤 토픽에 해당하는지를 본다. doc1의 모든 단어들은 토픽 A와 토픽 B에 50 대 50의 비율로 할당되어져 있으므로, 이 기준에 따르면 단어 apple은 토픽 A 또는 토픽 B 둘 중 어디에도 속할 가능성이 있다.

두번째 기준은 단어 apple이 전체 문서에서 어떤 토픽에 할당되어져 있는지를 본다. 이 기준에 따르면 단어 apple은 토픽 B에 할당될 가능성이 높다. 이러한 두 가지 기준을 참고하여 LDA는 doc1의 apple을 어떤 토픽에 할당할지 결정한다.
3. 잠재 디리클레 할당과 잠재 의미 분석의 차이
LSA : DTM을 차원 축소 하여 축소 차원에서 근접 단어들을 토픽으로 묶는다.
LDA : 단어가 특정 토픽에 존재할 확률과 문서에 특정 토픽이 존재할 확률을 결합확률로 추정하여 토픽을 추출한다.
'Natural Language Processing > 딥 러닝을 이용한 자연어 처리 입문' 카테고리의 다른 글
| [딥 러닝을 이용한 자연어 처리 입문]언어 모델(Language Model) (0) | 2021.03.17 |
|---|---|
| [딥 러닝을 이용한 자연어 처리 입문] 원-핫 인코딩(One-Hot Encoding) (0) | 2021.03.15 |
| [딥 러닝을 이용한 자연어 처리 입문]텍스트 전처리(text preprocessing) (0) | 2021.03.09 |
| [딥 러닝을 이용한 자연어 처리 입문]머신 러닝 워크플로우(Machine Learning Workflow) (1) | 2021.02.13 |
| [딥 러닝을 이용한 자연어 처리 입문]판다스 프로파일링(Pandas -Profiling) (0) | 2021.02.13 |